4.2 Clouds and Climate
Clouds have a large impact on radiative fluxes, impacting the net energy budget of the climate system, atmospheric heating rates, and energy exchange between the Earth's surface and the atmosphere. Cloud formation is organized by the large-scale atmospheric circulation and, in concert, cloud radiative forcing (CRF) is organized on large-scales. This makes clouds important both for dynamic circulations within the climate system and for model errors that degrade climate simulations, weather forecasts, and reanalysis data. CDC has used observations of cloud variability (e.g., from ISCCP) in a variety of diagnostic and modeling studies in order to improve our understanding of the role of clouds in the climate system.
4.2.1 A high order statistical cloud scheme for GCMs
Large scale models such as those used for weather and climate prediction represent the state of the atmosphere at a discrete set of grid points. These values are used to determine the rates of various processes occurring within the grid cell (how much cloud water is converted to rain, for example). But atmospheric properties vary at all spatial scales, so the properties within a grid cell are better represented by some distribution instead of a single value. If process rates depend non-linearly on the quantity in question, the rate averaged over each grid cell may be different than the rate computed from the grid cell average. The problem is most acute in clouds, especially when computing precipitation rates, as these processes are strongly non-linear in the amount of condensate. The sub-grid scale homogeneity bias in process rates can easily be a factor of two, and is likely the reason models need to be arbitrarily re-tuned at each change in spatial resolution.
CDC and GFDL scientists are working on a statistical cloud scheme that will account for unresolved spatial variability in the computation of process rates. Cloud resolving model simulations of convection over a mid-latitude land site are being used in two ways: to determine the distributions and parameters that best describe the variability in thermodynamic quantities that would not be resolved by a large-scale model, and to assess how these parameters change according to each physical process. Figure 4.6, for example, shows a time-height image of the standard deviation of total water content that would be computed from a model with 512 km grid size and 1 hour time step. Overlaid on this are contours of the detrainment from convective updrafts, which can be seen to increase the amount of variability.
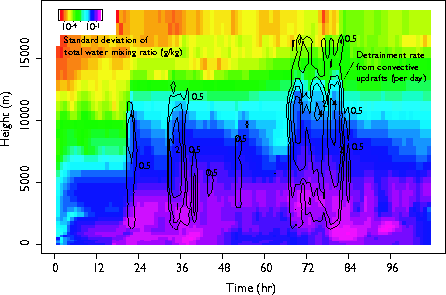
The eventual goal of this work, funded by the Department of Energy through the Atmospheric Radiation Measurement program, is to implement a statistical cloud in the GFDL Flexible Modeling System that predicts higher order moments of one or more thermodynamic quantities at each grid cell. Such a scheme should require substantially less arbitrary tuning than current models, and should be insensitive to changes in spatial and temporal resolution.
4.2.2 A parameterization of cloud overlap for general circulation models
How cloud overlap is specified in a general circulation model can have a large impact on radiative fluxes and heating rates. Current parameterizations of cloud overlap are also strongly sensitive to changes of vertical resolution. We have recently developed an overlap parameterization that is insensitive to changes of vertical resolution. In our scheme cloud overlap is described in terms of the correlation between horizontal cloudiness functions at different vertical levels. That correlation is assumed to decay exponentially with the separation distance between levels. This allows cloud overlap to be specified in terms of a single parameter, the decorrelation depth. While all pair-wise overlap fractions among cloudy levels can be calculated from the cloudiness correlation, those fractions can over-constrain the determination of the cloud distribution. It is found that cloud fraction in each level along with the overlap fraction among nearest neighbor cloudy levels is sufficient to specify the full cloud distribution. Our overlap parameterization has other desirable features that allow one to interpret the properties of complex cloud distributions in a simplified framework.
4.2.3 The seasonal cycle of cloud radiative forcing in the tropical Pacific
The radiative transfer model from NCAR's general circulation model CCM3 was modified to calculate monthly radiative fluxes and heating rates from monthly observations of cloud properties from ISCCP and temperature and humidity from ECMWF analysis. The modified model was efficient enough to allow a wide range of sensitivity tests. Seasonal variations of cloud radiative forcing were then investigated over the tropical Pacific. This quantifies the impact of clouds on atmospheric heating and on surface energy fluxes. The impact of CRF on surface winds, which also affect energy and momentum transfer at the surface, was then estimated in a linearized calculation of the tropical circulation forced by diabatic heating rates.
Typically, over the tropics, CRF represents approximately 20% of the annual variations of diabatic heating rates over convective locations and 50% or better at nonconvective locations. Seasonal variations of atmospheric CRF, when strong, tend to be in phase with those of total diabatic heating rates, indicating that clouds reinforce tropical circulations driven by latent heating. Cloud radiative forcing tends to have a stronger influence in the lower troposphere than at upper levels. It influences local circulations more than remote ones.
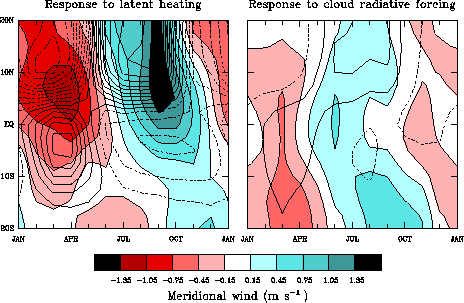
In the tropical east Pacific (85W to 105W), we investigated two mechanisms through which seasonal variations of CRF can impact seasonal variations of SST. The first is the `direct' impact of CRF at the surface, which acts as an energy source for the upper ocean. The second is the `indirect' impact of atmospheric CRF, which affects meridional surface winds that impact SST through coastal Ekman pumping that brings cool subsurface waters to the surface in the tropical east Pacific. CRF is a major contributor to the energy budget at the surface and in the atmosphere, particularly near and just south of the equator where seasonal variations of SST are strongest (Fig. 4.7a). The amplitudes of seasonal variations of surface CRF (Fig. 4.7c) are 20-30% as large as those of the net surface flux (Fig. 4.7b).
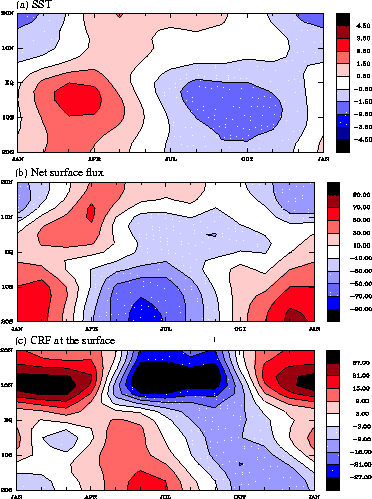
However, while the phase relationship between net surface flux and SST is consistent with the surface flux acting to force SST changes (i.e., surface fluxes lead SST by about 3 months), the phase of CRF is not consistent with it forcing SST changes. In fact, over locations where the seasonal cycle of SST is strongest, CRF tends to be out of phase with net surface fluxes, indicating that, if anything, the seasonal cycle of CRF damps SST variability. In contrast, the impact of CRF on meridional winds (relative to latent heating) is strong over the cold tongue (Fig. 4.8). Winds driven by CRF also have the correct phase to force the observed seasonal cycle of SST. So, to the extent that surface energy fluxes force the seasonal cycle of SST in the east Pacific, clouds are either unimportant or act to dampen SST variations. To the extent that upwelling driven by meridional winds is important, CRF, principally from seasonally varying stratocumulus, is very important.