Improving Week 2 Weather Forecasts Through "Re-Forecasting"
Researchers examine errors in old weather forecasts to improve skill of weather models

Susan Bacon, Winter 2004
Surface temperature forecast bias, St. Louis, Missouri | |
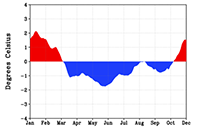
|
|
Click image for more detail | |
Decisions such as whether to carry an umbrella to work or whether to evacuate an area before a serious storm hits are a lot easier to make with the help of weather forecasts. But as any nightly news viewer knows, these forecasts are not perfect. In fact, the further into the future forecasts look, the more likely they are to be inaccurate. Now, two researchers at the ESRL Physical Sciences Laboratory are trying to improve the skill of forecasts one to two weeks ahead, where current forecasts have very little skill. But instead of modifying current computer forecast models or using more satellite data, PSL scientists Jeff Whitaker and Tom Hamill are examining the errors of old weather forecasts to get a clearer picture of the future.
Why is it so difficult for a supercomputer model using tens of millions of weather observations from satellites and radars and weather balloons to forecast the weather correctly in the first place? There two major sources of errors in weather forecasts, "chaos" and "model error." The longer the forecast, the larger these errors become.
Chaos is a mathematical buzzword describing the property that errors tend to grow exponentially in certain systems of equations. The evolution of the weather can be described with a very large set of equations, and numerical weather forecasts exhibits this chaos. Practically, what this means is that if a weather feature at is not described perfectly at the start of the numerical forecast, the initially small error will grow very rapidly and eventually ruin it. As the classic example goes, suppose the current state of the weather were known perfectly except for one unaccounted-for flap of a butterfly's wings in Asia. Incredibly, that initially small error in the computer representation of the weather can grow fast enough to render the forecast over the U.S. two weeks later nearly useless.
Another reason that weather models cannot make accurate medium-range weather forecasts is that the models themselves are imperfect codifications of the laws of nature. Although there are millions of equations for each model, there still is not enough computer resources available to represent all the small-scale details. The computer model of the weather thus treats the weather over you as being the same as the weather a block down the road. Further, all those little details -- how the wind is slowed blowing around your house, or how much water evaporated from the pond down the road -- these are only treated approximately, averaged over many houses and many ponds. Without a perfect description of every house and every pond, "model errors" are inevitably introduced.
Between model errors and chaos, a two-week forecast of the weather taken directly from the computer has nearly no skill at all. It is hard to determine what aspects of the weather remain predictable versus which are unpredictable. It can also be hard to determine whether, say, a cold, wet forecast indicates snow or just a systematic tendency for the model to be too cold or too wet.
Whitaker and Hamill address both these problems by generating a collection, or "ensemble" of 2-week computer forecasts for each day during the last 23 years. Each member of the ensemble was started from only a slightly different estimate of the starting weather condition.
The Whitaker and Hamill approach does not result in a perfect forecast, they found that they could make a much better forecast. They used the data set of old forecasts to understand and correct for the effects of chaos and model error in the current forecast. First, with an archive of old forecasts and the actual weather that happened, they were able to determine errors in the model, where it was consistently too warm or too cold, too wet or too dry. They could then adjust the current forecasts to back out these errors.
Second, by running an ensemble of forecasts, the consistency between these forecasts provided a way of distinguishing between situations that were predictable and those that were unpredictable. If the ensemble of forecasts were all very different from each other, then the forecast was largely unpredictable. However, in situations where the forecasts were all indicating similar temperature or precipitation anomalies, that consistency provided an indication that the forecast that day was predictable. Whitaker and Hamill demonstrated the validity of this technique using a relatively crude version of the weather forecast model that the National Weather Service (NWS) uses to make their forecasts. Only by using this simpler model was it computationally feasible to run the current ensemble of forecasts and ensembles for the past 23 years. Nonetheless, Whitaker and Hamill's forecasts proved to be more skillful than the operational week 2 forecasts produces by the NWS. These forecasts were produced subjectively with forecasters manually synthesizing different computer forecasts but without the aid of a database of past forecasts. As a result of Whitaker and Hamill's efforts, the NWS will be adopting their approach as a starting point for making week 2 forecasts.
As computer power grows each year, the complexity of weather forecast models will grow as well. But the take-home message of Whitaker and Hamill's research is that making a more complex computer model is not the end of the forecast process, but the beginning. The forecast model needs to be tested on lots of old weather scenarios. That way, before disseminating a forecast to the public, intelligent corrections can be made to remove model errors and determine what is predictable and what is not.