|
Numerical Simulation of Radar Scattering from Breaking Surface Gravity Waves
The small-slope approximation is working well for VV polarization at angles of incidence smaller than 60-70 degrees. For HH-polarization, even in this range of angles, it is necessary to take into account an additional contribution from steep waves in order for the resulting scattering cross section to be fitted with experimental data. The approach starts to be untenable at small grazing angles where diffraction on steep breaking waves becomes a dominating scattering mechanism.
A numerical 2-D scattering model was developed in our group to investigate basic features of low-grazing radar scattering from steep breaking waves [1]. Currently, we are working on developing more advanced 3-D scattering models.
The numerical 2-D model includes a model of the rough surface and the electromagnetic scattering model. The model of the rough surface deals with two types of waves: large-scale periodic non-linear gravity waves, and random short-scale capillary-gravity waves riding atop longer waves. First, the hydrodynamic equations for potential surface waves including surface tension but without viscosity are solved. The approach yields temporal evolution of the profiles of the steep and breaking waves having non-single-valued profiles. As a result, it becomes possible to follow through various stages of wave breaking: steepening, cresting, involution, and jetting (Fig. 2). The short waves are described statistically by a stationary and spatially uniform power-law spectrum with a lower cutoff spatial frequency three times smaller than the spatial frequency of the EM wave.

Figure 2. Wave profile evolution.
The electromagnetic scattering model is concerned with solving a 2-D Helmholtz equation with impedance boundary conditions applied to the profiles of large-scale gravity waves obtained by the hydrodynamic model described above. As a result, the scattering amplitudes of EM waves for vertical and horizontal polarizations at various angles of incidence and scattering are calculated. Using surface fields obtained at this step as sources for the small-perturbation theory, Bragg-type scattering on small-scale roughness is calculated and added to the cross sections caused by steep breaking waves.
Calculations have been performed for 1.0-m wavelength surface waves and a 4.65-cm EM wavelength and the two orthogonal polarizations for various incident and scattering angles. For a backscattering regime and for the upwind, front-face incidence at grazing angles 20°, the results evidently support observable behavior of backscatter with an expected spike-like increase of HH-pol. that exceeds VV-pol. when the surface wave is passing the cresting stage and goes into involution (Fig. 3). Onset of jetting leads to a relative subsidence of backscatter with HH-pol. becoming smaller than VV-pol. Also, for the strongly non-linear waves alone, the corresponding Doppler spectrum at HH-pol. is broader than for VV-pol.

Figure 3. Changes in cross sections during the evolution of the breaking wave. The last 0.1 s is characterized by a spike for HH-polarization.
To better understand the physical processes behind this scattering phenomenon, we have also undertaken ray tracing simulations based on geometric optics considerations (Fig. 4).
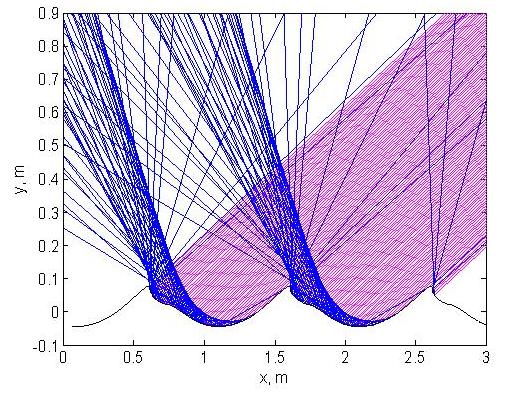
Figure 4. An example of ray tracing simulations in the case of a breaking wave.
Comparison between scattering cross sections obtained using full-wave and ray simulations demonstrates a fair agreement between two approaches for smoother surfaces and steeper incidence. For a given type of surface profile, better agreement is obtained for the forward scattering directions than for the backscattering directions. The ray simulation for the backscattering direction even with multiple reflections taken into account does not reproduce well the HH/VV ratio observed in the full-wave solution. This indicates that diffraction plays an important role in microwave radar backscattering from breaking waves.
There are many still unanswered questions in the ocean radar scattering phenomenon, especially with respect to multiple scattering at grazing angles, to a more complex situation with 3-D modeling of EM scattering. Our ultimate goal is to apply the knowledge obtained to better parameterization of the process of the air-sea interaction. We continue to work toward this goal.